[논문리뷰] BALM: Bundle Adjustment for Lidar Mapping
BALM: Bundle Adjustment for Lidar Mapping 논문을 정리한 포스트입니다.
2021년에 나왔으며 저자는 Zheng Liu와 Fu Zhang 입니다.
깃허브는 이후에 나온 BALM 2.0까지 합쳐져 있으며, BALM-old 폴더에서 본 논문의 코드를 확인할 수 있습니다.
이후에 나온 LiDAR BA 관련 논문은 아래를 참고해주세요.
BALM 2.0 (2022)
Hierarchical LiDAR BA (2023)
1. BA in LiDAR SLAM
2. BALM Contribution
3. Related Work
4. BALM Formulation and Derivatives
A. Direct BA Formulation
B. The Derivatives
C. Second Order Approximation
5. Adaptive Voxelization
6. LOAM with Local BA
7. Experiments
A. Livox Horizon
B. Livox MID-40
C. Velodyne VLP-16
D. Running Time
8. Future Work
1. BA in LiDAR SLAM
BA는 3D 구조(feature point들의 location)와 카메라 포즈를 동시에 최적화하는 기법이다. 키프레임에 대한 local BA on sliding window는 Visual SLAM에서 많이 사용되는 기법이고, drift를 낮추는 데 매우 효과적이다. SfM, visual SLAM, visual-inertial navigation과 같은 다양한 visual application에 적용된다.
LiDAR SLAM에서는 LiDAR pose와 global 3D point-cloud map을 동시에 결정하는 문제로 정의할 수 있다.
기존에 널리 사용되는 point cloud registration method (ICP, GICP, NDT, surfel based ...) 는 연속적인 두 포인트 클라우드 간의 정합만을 다룬다는 한계점이 있다. 따라서 dift가 누적된다. 또한 degeneration이 발생하는 featureless 환경이나 small FoV의 LiDAR 때문에도 registration error가 누적된다. 이러한 drift를 줄이기 위한 방법 중 하나로 local BA를 수행할 수 있다. LiDAR scan에 대해 sliding window를 취함으로써 새로운 스캔에 대한 정보를 기반으로 과거 스캔에 다시 접근할 수 있다. 그러나 LiDAR 포인트 클라우드는 매우 sparse 하고 non-repetitive 하다는 성질이 있으므로 정확한 point matching이 불가능하다.
Direct depth measurement로 인해 LiDAR BA가 Visual BA보다 간단해보이지만, formulation은 더 복잡하다. Visual SLAM에서는 높은 해상도 이미지가 measurement 이고, 각 픽셀은 공간에서 single feature에 해당한다. Projected feature location과 이미지 상에서의 실제 location의 차이를 최소화하도록 공식화한다. LiDAR BA는 feature point에서 matched edge or plane까지의 거리를 최소화 한다.
2. BALM Contribution

1. BA에서 feature를 제거해 BA 결과가 scan pose에만 dependent 하게 한다.
Visual SLAM과 기존 LiDAR SLAM에서의 plane adjustment 방법에서는 feature가 pose에 따라 co-determined 되어야 했다. feature location과 카메라 포즈를 동시에 푸는 visual BA와 달리, closed-form solution으로 LiDAR BA의 feature parameter를 풀어 스캔 포즈에 대해서만 BA 최적화 한다.
Optimization dimension을 크게 줄여 large-scale dense plane and edge features를 사용할 수 있다.
2. 빠른 최적화를 위해 cost function을 analytical 2차 도함수(closed-form)를 도출한다.
Cost function의 gradient와 Hessian mtx를 스캔 포즈에 대해 분석적으로(analytically) 유도한다.
왜 2nd order 일까? Second-order Newton iteration method 와 Gauss-Newton method는 다르다. Eigenvalue는 square of distance와 같으므로 sqaure term이 있는 Gauss-Newton method를 사용하면 fourth power of distance를 최적화 하는 것이다. 따라서 수렴이 느리다. 이때 square term이 없는 Second-order Newton method를 사용하면 square of distance이므로 4-5번의 iterations 만에 수렴할 수 있다.
3. feature correspondence를 효율적으로 찾기 위해 novel adaptive voxelization 기법을 사용한다.
4. map refinement를 수행하는 LOAM back-end에 통합해본 결과, 효과적이다.
LOAM mapping 결과를 initial value로 하여 local BA를 수행했다. Fig. 2의 (b)에서 (a)와 비교해 drift가 확연히 줄어든 것을 확인할 수 있다. 20개의 temporal point cloud 스캔에 대해, back-end에서 10Hz의 실시간임에도 local BA가 매우 빠르게 수행되었다. spinning LiDAR와 small FoV의 LiDAR에서도 좋은 성능을 보인다.

(Video : https://www.youtube.com/watch?v=d8R7aJmKifQ)
3. Related Work
BALM은 Multi-View Registration task와 비슷하다.
1. ICP 기법 확장
초기에는 ICP 방법을 확장하였다. cost function은 임의의 두 스캔에서 두 corresponding points 사이 거리의 합 또는 corresponding surface 사이의 거리를 사용한다. 이러한 방법은 depth camera와 같은 dense 3D 스캔에 잘 작동하지만, 정확한 point 또는 surface matching이 필요해 LiDAR 포인트 클라우드에는 적용이 어렵다.
2. Standard pairwise scan registration 기법
Standard pairwise scan registration 기법을 이용해 overlap이 있는 두 스캔을 정합한다. 그후 얻은 relative pose를 measurement로 사용하여 pose graph를 구성한다. graph optimization을 통해 포즈를 결정할 수 있다. 하지만 overlap을 가진 모든 스캔들 사이에서 repeated pairwise scan registration을 수행해야 한다. 또한 포인트 클라우드 맵을 직접적으로 최적화하지 않아 mapping consistency를 제한한다.
3. sparse points의 alignment 품질을 효과적으로 평가하는 metric
LiDAR BA(또는 multi-view registration)의 difficulty는 모든 스캔에서 sparse 포인트의 alignment 품질을 효과적으로 평가하는 동시에 효율적인 최적화를 허용하는 metric을 정의하는 데 있다. Correlation (or entropy)-based scan registration은 자연스럽게 multiple scans으로 확장되지만, 모든 point pair에 대해 correlation을 계산해야 하기 때문에 Careful engineering 또는 GPU 가속이 필요하다. 계산 부하를 낮추기 위해 최근 연구에서는 plane feature에서만 BA을 수행하였다. 이러한 연구는 plane parameter와 스캔 포즈를 동시에 최적화하여 high-dimension이다. 대조적으로, BALM은 plane과 edge를 모두 고려하고 BA 최적화 전에 closed-form으로 두 feature을 분석적으로 푼다. 결과 BA는 스캔 포즈에 대해서만 고유값을 최소화하도록 감소한다. 고유값을 비용 함수로 사용하여, 분석적으로 2차 도함수를 도출하고, 최적화 속도를 높이기 위해 매우 효율적인 Gauss-Newton 방법을 활용한다.
4. Sliding Window Optimization
슬라이딩 윈도우 최적화를 사용한 LOAM에서는 기존 맵에 슬라이딩 윈도우 상의 각 스캔을 정합하여 라이다 스캔의 슬라이딩 윈도우를 최적화한다. 이는 기본적으로 슬라이딩 윈도우 내 스캔 간의 모든 동시 제약 조건(concurrent constraints)을 무시하므로 최적이 아닌(suboptimal) 솔루션이다. 하지만 이러한 모든 제약 조건을 고려하면 repeated pairwise scan registration으로 이어진다. Droeschelet 의 연구는 multi-view registration이 가능하지만 메모리 또는 계산 비용이 너무 많이 드는 multi-resolution occupancy grid map을 사용한다.
5. BAML
최적화에서 feature(both edge and plane) parameter를 제거하여 최적화 dimension을 크게 줄이고, 수렴 속도를 크게 높이는 2차 최적화를 통해 많은 수(예: 수백 개)의 feature을 최적화하는 경우에도 BA를 real-time으로 수행할 수 있다.
또한, 일반적으로 raw 포인트 클라우드에서 평면을 segment하고 일반적으로 실제 plane feature을 인정하는 이전 방법과 달리, segment 없이 plane과 edge feature을 모두 match하는 adaptive voxelization를 제안한다. 이 방법은 large planes(ground, wall)와 small planar patches(tree crowns)가 있는 다양한 환경에도 적용할 수 있다.
4의 작업과 비교하여 BALM은 슬라이딩 윈도우 또는 맵에서 모든 스캔 간의 모든 제약 조건을 고려하고 매우 효율적이다.
4. BALM Formulation and Derivatives

A. Direct BA Formulation
$M$개의 스캔으로부터 얻어졌지만 모두 같은 feature (plane or edge)에 해당되는 sparse feature points $ p_{f_i} (i=1,...,N)$ 그룹이 있다. (Fig. 3 참고)
- $i$번째 feature point는 $s_i$ 번째 스캔에서 얻었다. $s_i \in \left\{1,...,M\right\}$
- $M$개 스캔의 포즈 $T=(T_1,...,T_M)$
- $T_j=(R_j,t_j)\in SO(3) \times \mathbb{R}^3$, $j \in \left\{ 1,...,M \right\}$
- $p_i$ : global frame의 feature point
$$ \begin{align*} p_i=R_{s_i}p_{f_i}+t_{s_i};i=1,...,N \tag{1} \end{align*} $$
이전에 정의했던 것과 같이, LiDAR BA는 $M$ scans의 pose들과 global 3D point cloud map을 함께 결정한다. 이제 3D map은 single feature(edge or plane)이고, 그러므로 BA는 poses $T$와 single feature의 위치를 함께 결정하는 문제로 줄어든다. single feature는 feature 위의 point $q$와 unit vector $n$으로 표현되고 이때 $n$은 plane의 normal vector 또는 edge의 direction이다.
plane feature의 경우 direct BA formulation은 각 plane feature point $p_i$(depends on the pose $T_{s_i}$)에서 plane까지의 summed squared distance을 최소화한다. $\lambda_k(A)$는 mtx $A$의 $k$번째로 큰 eigenvalue이고 $u_k$는 그에 해당하는 eigenvector이다. 즉 가장 작은 eigenvalue $\lambda_3$을 최소화 한다. 이해가 안 된다면 아래 covariance matrix에서 고유벡터와 고유값이 어떤 의미를 가지는지 확인해보자.
$$ \begin{align}(T^*,n^*,q^*)
& = arg \underset{T,n,q}{min} \frac{1}{N} \sum^{N}_{i=1}
(n^T(p_i-q))^2
\\ &=arg \underset{T}{min} \underset{=\lambda_3(A);\text{if } n^*=u_3,q^*=\bar{p}}{(\underbrace{\underset{n,q}{min}\frac{1}{N} \sum^{N}_{i=1}
(n^T(p_i-q))^2)}}) \tag{2} \end{align} $$
$\bar{p}$는 동일 feature에 대한 $p_i$의 평균이고, $A$는 $p_i$의 covariance mtx이다.
[ covariance matrix 에서 고유벡터, 고유값의 의미 ]
데이터셋을 하나의 차원으로 줄이기 위해서는 unit vector $u$를 골라 각 데이터 포인트 $x_i$를 $u$에 대해 projection 한 $u^T x_i$로 대체한다. 이때 데이터 포인트를 다양하게 잘 유지하는 $u$를 골라야 한다. 그런데 만약 데이터가 한 선을 따라 존재했고 그 선에 orthogonal한 $u$를 골랐다면 모든 데이터 포인트들은 같은 값으로 projection 되어 모든 정보를 잃게 될 것이다. 따라서 $u^T x_i$의 분산을 최대화 하는 $u$를 골라야 한다. original data points $x_i$의 공분산 행렬이 $\Sigma$이면 새로운 데이터 포인트들의 분산은 $u^T \Sigma u$이다. $\Sigma$가 symmetric하기 때문에 $u^T \Sigma u$를 최대화 하는 unit vector $u$는 가장 큰 고유값의 고유벡터이다.
PCA는 데이터에서 의미있는 축을 찾아낸다. 각 축을 주성분이라고 하며, 주성분의 수는 차원의 수와 같다. PCA는 어떠한 축이 중요한지 찾아준다. 공분산 행렬에서 고유벡터와 고유값을 찾는 것은 데이터의 주성분을 찾는 것과 같다. 고유벡터는 행렬이 어떤 방향으로 힘을 가하는지를 표현하는데, 이것은 데이터가 어떤 방향으로의 분산이 가장 큰지 구하는 것과 같다. 공분산 행렬의 고유벡터는 데이터가 어떤 방향으로 분산되어 있는지를 나타내고, 고유값은 각 축에 대한 공분산 값이다. 이 문제에서는 3D 벡터의 공분산 행렬이기에 3개의 주성분이 존재한다.
$$ \begin{align}
\bar{p}=\frac{1}{N} \sum^{N}_{i=1}
p_i ; A=\frac{1}{N} \sum^{N}_{i=1}
(p_i-\bar{p})(p_i-\bar{p})^T
\tag{3} \end{align} $$
edge feature의 경우 plane feature와 비슷하게 각 edge feature point $p_i$에서 edge까지의 summed squared distance를 최소화한다. $Tr(A)=\frac{1}{N} \sum^{N}_{i=1} ||p_i-q||^2_2$ 는 A의 trace를 뜻한다. 즉 가장 큰 고유값 $\lambda_1$을 최대화한다. $min$ 연산자를 사용했으므로 $\text{Tr}(A)$에서 $\lambda_1$을 뺀 값, 즉 $\lambda_2 + \lambda_3$로 표현할 수 있다.
$$ \begin{align} (T^*,n^*,q^*)
& =arg \underset{T,n,q}{min} \frac{1}{N} \sum^{N}_{i=1}
||(I-nn^T)(p_i-q)||^2_2
\\ &=arg \underset{T}{min} \underset{=Tr(A)-\lambda_1(A)=\lambda_2(A)+\lambda_3(A);\text{if }n^*=u_1,q^*=\bar{p}}{(\underbrace{\underset{n,q}{min}\frac{1}{N} \sum^{N}_{i=1}
||(I-nn^T)(p_i-q)||^2_2}})
\tag{4} \end{align} $$
위의 두 공식에서 optimal point $q^*$는 unique하지 않다. point는 plane 내부 또는 edge를 따라 자유롭게 이동할 수 있기 때문이다. 하지만 이는 결과 cost function을 최적화 하는 데는 영향을 미치지 않는다. 또한 두 식은 BA 이전에 optimal feature(plane or edge) parameter를 분석적으로 얻을 수 있으며 결과적인 BA 문제는 poses $T$에만 의존한다. 이는 3D 포인트 클라우드 map(즉, plane or edge features)은 스캔 포즈를 알면 결정된다는 직관과 일치한다. 게다가 poses $T$에 대한 최적화는 (3)에서 mtx $A$의 eigenvalue을 최소화하도록 감소한다. 즉, BA는 다음을 최소화한다.
(스스로에 대한 공분산 행렬의 고유값이 0이라는 것은 축에 대한 분산이 0, 즉 평균이 0이라는 것이다.)
$$ \begin{align} \lambda_k(p(T)) \tag{5} \end{align} $$
$T$에 대해, $p=[p^T_1\cdots p^T_N]^T$은 같은 feature에 해당하는 모든 feature points의 벡터이다.
(5)을 cost로 하는 효율적인 최적화를 위해, 분석적으로 closed-form derivatives를 pose $T$에 대해 2차 도함수까지 유도한다. chain rule 때문에, 먼저 point vector $p$에 대해 derivatives를 유도한다.
B. The Derivatives
Theorem 1 : points group에 대해, $p_i (i=1,...,N)$와 (3)에 정의된 covariance mtx $A$가 있다. $A$는 eigenvector $u_k(k=1,2,3)$에 해당하는 고유값 $\lambda_k$을 가지고 있다. $\bar{p}$는 (3)에서 $N$ points의 평균이다.
$$ \begin{align}
\frac{ \partial \lambda_k}{ \partial p_i}=\frac{2}{N} (p_i-\bar{p})^Tu_ku^T_k \tag{6}
\end{align} $$
[유도 과정]
- point $ p_i = \begin{bmatrix} x_i & y_i & z_i \\ \end{bmatrix}^T$
- eigenvector matrix $U = \begin{bmatrix} u_1 & u_2 & u_3 \\ \end{bmatrix}^T$
- $p$ 는 $p_i$ 의 한 element 로 $x_i, y_i, z_i$ 중 하나이다.
정의에 의해 아래와 같다. $U^TU=I$임을 이용해 (15)에서 (17)을 유도할 수 있다.
$$ \begin{align} \Lambda=U^TAU \tag{15} \end{align} $$
$$\begin{align}
\frac{\partial \Lambda}{\partial p}
=\frac{\partial \Lambda}{\partial p}=(\frac{\partial U}{\partial p})^TAU
+U^T\frac{\partial A}{\partial p}U
+U^TA\frac{\partial U}{\partial p}
\tag{16} \end{align}$$
$$ \begin{align}
U^TA=\Lambda U^T ; AU=U \Lambda
\tag{17} \end{align} $$
(17)을 (16)에 대입하면
$$ \begin{align}
\frac{\partial \Lambda}{\partial p}
=U^T \frac{\partial A}{\partial p}U
+\Lambda \underset{C^p}{\underbrace{U^T \frac{\partial U}{\partial p}}}
+\underset{C^p}{\underbrace{(\frac{\partial U}{\partial p})^T U} \Lambda}
\tag{18} \end{align} $$
$U$는 orthogonal 하므로 $p$에 대해 편미분 하면
$$ U^T\frac{\partial U}{\partial p} + ( \frac{\partial U}{\partial p})^T U=0
\Rightarrow C^p+(C^p)^T=0 $$
$C^p$가 diagonal elements가 0인 skew symmetric matrix 이고, $\Lambda$가 diagonal matrix이므로 (18)의 RHS의 마지막 두 항을 합치면 diagonal positions에 대해 0이다. (18)에서 diagonal element들만 고려하면 다음과 같다.
$$ \frac{\partial \lambda_k}{\partial p}
= u^T_k \frac{\partial A}{\partial p} u_k
= \frac{\partial u^T_k A u_k}{\partial p} \quad (k=1,2,3)$$
두번째 항의 벡터 $u_k$는 항상 일정하게 관측된다. $lambda_k$를 $p_i$의 모든 element들에 대해 편미분 한 것을 stack 하면 아래와 같다.
$$\begin{align}
\frac{\partial \lambda_k}{\partial p_i}
= \begin{bmatrix}
\frac{\partial u^T_kAu_k}{\partial x_i}
& \frac{\partial u^T_kAu_k}{\partial y_i}
& \frac{\partial u^T_kAu_k}{\partial z_i}\\
\end{bmatrix}
= \frac{\partial u^T_kAu_k}{\partial p_i}
\tag{18} \end{align}$$
(3)의 정의에 따라
$$\frac{\partial p_j}{\partial p_i}=I,(i=j) \quad\quad \frac{\partial p_j}{\partial p_i}=0,(i\neq j)$$
이제 다음을 얻을 수 있다.
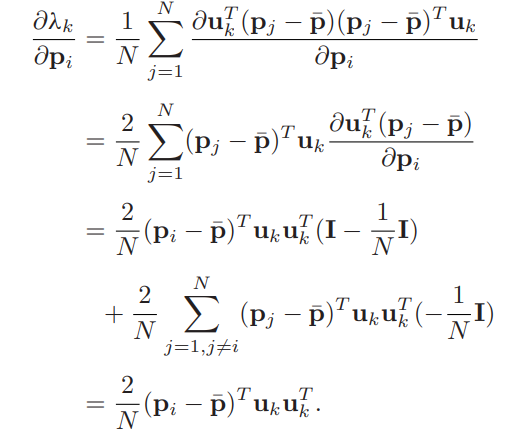
Theorem 2 : points group에 대해, $p_i(i=1,...,N)$와 (3)에서 정의된 covariance mtx $A$가 있다. $A$는 고유벡터 $u_k(k=1,2,3)$에 해당하는 고유값 $\lambda_k$를 가지고 있다고 가정한다. $i \neq k$이면 $\lambda_i \neq \lambda_k$이다.

[유도 과정]
포인트 두 개를 고려해보자.
- point $p_i = \begin{bmatrix} x_i & y_i & z_i \\ \end{bmatrix}^T$
- point $p_j = \begin{bmatrix} x_j & y_j & z_j \\ \end{bmatrix}^T$
- $q$ 는 $p_j$ 의 한 element 로 $x_j, y_j, z_j$ 중 하나이다.
고유벡터 행렬 $U$가 orthogonal 하므로
$$ U^T \frac{\partial U}{\partial q}
+ (\frac{\partial U}{\partial q})^T U = 0 $$
이때
$$C^q = U^T \frac{\partial U}{\partial q},\quad
C^q + (C^q)^T = U$$
$C^q$의 diagonal element들은 0이다. (18)과 비슷하지만, $p$를 $q$로 대체한다.
$$\begin{align} \frac{\partial \Lambda}{\partial q}
= U^T \frac{\partial A}{\partial q} U + \Lambda C^q - C^q \Lambda
\tag{20} \end{align}$$
$\Lambda$가 diagonal 하므로 (20)의 off-diagonal element들에 대해 $\frac{\partial A}{\partial q} U$은
$$ 0 = u^T_m \frac{\partial A}{\partial q} u_n + \lambda_m C^q_{m,n} - C^q_{m,n} \lambda_n $$
$C^q_{m,n}$ 은 $\lambda_m \neq \lambda_n$일 때 $C^q$의 $m$행 $n$열 element이다.
$$\begin{align}
C^q_{m,n}=\left\{\begin{matrix}
\frac{1}{\lambda_n - \lambda_m} u^T_m \frac{\partial A}{\partial q} u_n &, m \neq n \\
0 &, m=n \\
\end{matrix}\right.
\tag{21}\end{align}$$
$C^q$의 정의에 따르면,
$$ \frac{\partial u_k}{\partial q} = \frac{\partial U e_k}{\partial q} = UC^q e_k $$
$e_k$는 $k$-th element가 1이고 나머지는 0인 $3 \times 1$ 벡터이다. $p_j$의 모든 element들에 대해 $u_k$를 편미분 하여 stack 하면

$F^{p_j}_{m,n}= \begin{bmatrix}
C^{x_j}_{m,n} & C^{y_j}_{m,n} & C^{z_j}_{m,n} \\
\end{bmatrix}_{1 \times 3}, m,n \in \{ 1,2,3 \}$ 라고 정의하자. (21)과 같이 $C^{x_j}_{m,n}$의 각 element에 대해 stack 하면

벡터 $u_m$와 $u_n$ 은 constant하게 관측된다.
(19)에서 미분한 것과 비슷하게, $F_{m,n}^{p_j}$ form으로 얻을 수 있다.
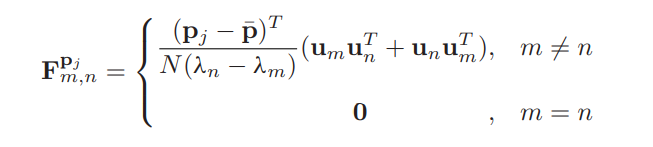
그러므로 (22)는 다음과 같이 된다.

(19)의 $\frac{\partial \lambda_k}{\partial p_i}$와 (23)의 $\frac{\partial u_k}{\partial p_j}$를 참고하면

$u_k (p_i - \bar{p})^T$는 행렬이지만 $u_k^T (p_i - \bar{p})$은 스칼라임을 기억하자. 더불어,

따라서 (24)는 (7)로 정리된다.
C. Second Order Approximation
이제 cost function (5)을 아래와 같이 2차 도함수까지 근사할 수 있다.

$J(p)$는 (6)의 $i$번째 element의 자코비안 mtx 이고, $H(p)$는 (7)의 $i$번째 행, $j$번째 열 element에 대한 Hessian mtx이다.

(8)에 (12)를 대입하면 다음과 같다.

마지막으로, Levenberg-Marquardt (LM) 방법을 사용해 cost $\lambda_k$를 (13)의 2차 근사로 반복적으로 근사해 최소화한다. 각 iteration에서 solution은 (14)로부터 풀어진다. $\mu$는 LM 기법으로부터 정해진 step size이다.
(2nd-order approximation LM optimization method 공식의 유도)

5. Adaptive Voxelization
4에서, BA 공식에서 같은 feature에 대해서 모든 feature points를 찾아야 한다. 그러기 위해 adaptive voxelization method를 새롭게 제안한다. 각 스캔에서 LOAM odometry 등을 이용해 rough initial pose를 얻을 수 있다고 가정하고, 3D 공간을 default size (e.g., 1m) 로 반복해서 복셀화 한다. 현재 voxel 내에서 모든 스캔으로부터의 모든 feature points가 하나의 plane 또는 edge 위에 있으면(e.g., point covariance mtx (3)의 eigenvalue 계산), 현재 voxel은 feature points와 함께 메모리에 유지되고, 그렇지 않으면 현재 voxel은 8개의 octants로 나누어져 minimal size(e.g., 0.125m)에 달할 때까지 각 octant를 체크한다. 각 voxel이 환경에 adaptive하게 여러 size를 가진 voxel map을 생성한다. 각 voxel은 하나의 feature에 해당하므로 (13)과 같이 하나의 cost item이다. Fig. 4(a) voxel map의 예시이다.

adaptive voxelization은 많은 장점을 가진다.
- 옥트리와 같은 기존 데이터 구조와 자연스럽게 호환되므로 구현 및 효율성이 크게 향상될 수 있다.
- 포함된 feature points가 같은 plane이나 edge에 있을 때 early termination이 발생할 수 있으므로, LOAM 같이 일반적으로 feature points에 full Kd-tree를 구성하는 것보다 더 효율적이다. 환경에 큰 planes이나 긴 edges가 있을 때 매우 효율적이다.
- adaptive voxels으로 구성된 map은 LiDAR odometry에서 feature correspondences를 찾는데 시간이 적게 걸린다. LOAM처럼 가장 가까운 point들을 찾는 대신, feature point가 속해 있거나 옆에 있는 voxel만 찾으면 된다.
구현에 있어서, edge features와 planar features 두 개의 voxel map을 구성한다. voxel map은 구조 상 octree 구조에 적합하다. octree의 depth를 감소시키기 위해 Hash table로 인덱싱된 octree set을 사용한다. (Fig. 4(c) 참고) 각 octree는 공간 상에서 default voxel size(e.g., 1m)의 non-empty cube에 해당한다. 각 octrees는 공간 상에서 각 cube의 geometry에 따라 다른 depth를 가진다. 하나의 octree 안의 각 leaf node (i.e., a voxel)는 모두 같은 feature(palne or edge)에 해당하는 feature point들을 저장하고 있다.
Remark 1: voxel이 너무 많은 points들을 포함하고 있다면 (8)의 Hessian mtx은 매우 고차원이게 되므로 이런 경우 same scan으로부터 points들을 평균화 할 수 있다. 평균화 된 points는 더 적은 수를 가지고 raw feature points에 의해 결정된 동일한 plane에 위치한다. 연산량을 크게 줄이면서도 mapping consistency는 저하되지 않는다.
Remark 2 : Theorm 2에서 계산되는 Hessian mtx는 $i \neq k$일 때 $\lambda_i \neq \lambda_k$ 여야 한다.$\lambda_k$의 algebraic multiplicity가 1보다 큰 voxel에 대해서는 스킵한다.
Remark 3 : edge와 plane feature 로 곡면와 같은 non-planar feature도 잘 표현할 수 있어야 한다. voxel map을 finer level에서 구성하고 포함된 points들이 같은 plane에 속해있는지 판단할 때 더 큰 variance를 허용함으로써 non-planar feature로 확장할 수 있다.
Remark 4 : 반복적인 분할을 멈추기 위해 두 가지 조건을 설정한다. tree의 maximal depth / voxel 내부의 최소 points 수
6. LOAM with Local BA

BA formulation과 optimization을 LOAM framework에 통합한다. feature extractoin, odometry, map-refinement 세 개의 thread가 병렬로 구성된다. feature points 의 새로운 스캔이 입력되면 odometry는 새로운 스캔을 기존 맵에 정합함으로써 LiDAR pose를 추정한다. 각 feature point가 map에서 가장 가까운 points에 매치되는 기존 LOAM과 달리 adaptive voxel map을 사용해 매칭 과정이 빠르다. 구체적으로, voxel map을 구성할 때 center point 와 voxel의 plane(or edge)의 normal (or direction) vector를 계산한다. 새로운 스캔의 각 포인트에 대해 가장 가까운 voxel (center point로 표현) 의 feature 까지의 거리를 계산한다.
Odometry로 새로운 스캔을 러프하게 global frame에 정합시키고 voxel map으로 넣는다. 새로운 스캔의 각 포인트에 대해 포함된 voxel을 찾고 이 포인트를 해당 옥트리의 leaf node에 추가한다. 기존 map에서 복셀을 찾지 못하면 새로운 octree를 생성해 Hash table에 root를 인덱싱하고 포인트를 root node에 추가한다. 새로운 스캔의 모든 feature point들이 기존 octree의 leaf node 또는 새롭게 생성된 octree의 root node에 분포되면 voxel map을 업데이트 한다. node (leaf or root)의 포인트들이 single feature(plane or edge)를 표현하지 않으면 노드를 8개로 나누고 각각을 체크한다.
새로운 스캔을 특정 수 만큼 voxel map에 넣으면 map-refinement가 수행된다. map-refinement는 LiDAR pose들에 local BA on sliding window를 수행한다. sliding window 안의 points(i.e., $P_{\text{sw}}$)를 포함하는 임의의 복셀은 (2) 또는 (4)와 같은 cost item을 구성하는 데 사용된다. 그후, map-refinement는 모든 관련 복셀로 구성된 total cost의 2차 근사 (13)를 반복적으로 최소화 한다. 이를 통해 sliding window 내의 LiDAR pose들을 조정한다. 업데이트된 pose로 포함된 복셀들의 center points와 normal vectors를 업데이트 한다.
sliding window가 다 차면 오래된 스캔들의 point들은 map points $P_{\text{fix}}$로 통합된다. point covariance mtx (3)의 좋은 성질은 recursive form이 존재한다는 것으로[1], slliding window 외부의 모든 포인트가 raw point를 저장하지 않고 몇 개의 컴팩트한 mtx와 vector로 요약될 수 있다. (Fig. 5의 하단 참고) 통합된 포인트들 $P_{\text{fix}}$는 odometry와 map-refinement 를 위해 voxel map에 유지된다.
7. Experiments
LOAM에 BALM을 적용했다. LiDAR odometry는 10Hz, map-refinement는 5개 스캔마다 수행되어 2Hz이다. sliding window는 최근 20개 스캔에 대해 적용한다.
A. Livox Horizon
outdoor 환경에서 20분 동안 걸어 시작점으로 돌아오는 데이터셋에 대해, Fig.6에서 LOAM과 BALM을 비교할 수 있다.
센서를 손으로 들고 계단을 따라 걸은 indoor 실험은 Fig.2에서 볼 수 있다.


B. Livox MID-40
small $40^o$ FoV. LOAM에서 지그재그 모양의 포즈 궤적을 만들어낸다.

C. Velodyne VLP-16


D. Running Time
BALM이 LOAM보다 빠르다. local BA는 odometry처럼 거의 real-time으로 구현된다.

8. Future Work
LOAM에서 로컬 BA의 현재 구현은 temporal 스캔의 슬라이딩 윈도우를 사용하므로 large overlap을 공유하는 인접 스캔에서 redundant information가 발생한다. 또한 좋은 initial pose alignment가 필요한 것은 voxelization의 단점이다. 그러나 현재 LiDAR odometry는 모션 왜곡을 보상하거나 모션 모델을 활용하지 않고 간단한 scan-to-map front-end를 사용한다. 따라서 future work는 local 슬라이딩 윈도우에서 keyframe을 채택하고 모션 모델을 추가로 통합할 것이다. 또한, BALM을 LOAM 이 아닌 다른 global mapping 및 extrinsic calibration에도 사용할 수 있다.
Reference
[1] "A fast, complete, point cloud based loop closure for LiDAR odometry and mapping", Jiarong Lin and Fu Zhang
[2] 공분산 행렬에서 고유벡터가 주성분인 이유 (https://math.stackexchange.com/questions/23596/why-is-the-eigenvector-of-a-covariance-matrix-equal-to-a-principal-component)
[3] 공분산 행렬에서 고유값, 고유벡터의 의미 (https://blog.naver.com/angryking/221206754322)