[논문 리뷰] LOAM : Lidar Odometry Mapping in Real-time
1. LOAM
2. Related Work
3. Notations and Task Description
4. System Overview
A. LiDAR Hardware
B. Software System Overview
5. LiDAR Odometry
A. Feature Point Extraction
B. Finding Feature Point Correspondence
C. Motion Estimation
D. LiDAR Odometry Algorithm
6. LiDAR Mapping
7. Experimetns
A. Indoor & Outdoor Tests
B. Assistance from an IMU
C. Tests with KITTI Datasets
1. LOAM
LOAM은 LiDAR SLAM의 기본이 되는 알고리즘으로, 3D lidar로부터 수신한 포인트 클라우드로 ego-motion 을 추정하고 맵을 구성한다.
- 6-DoF의 2-axis 라이다를 모터로 회전시켜 3D 라이다처럼 사용한다.
- 높은 정확도의 ranging/inertial 관측이 없어도 낮은 drift와 연산 복잡도를 가진다.
- 빠른 인덱싱을 위해 KD-tree 사용
- loop closure는 사용하지 않는다.
- IMU 사용이 가능한 경우, IMU에 칼만 필터를 적용해 추정한 orientation을 motion priori로 사용해 high frequency motion을 보정할 수 있다.
Odometry와 Mapping 두 알고리즘으로 나누어서 수행하여 실시간 SLAM이 가능하다.
- Odometry 알고리즘 : 10Hz로 라이다의 속도를 추정하고 포인트 클라우드의 distortion 보정 (high frequency, low fidelity)
- Mapping 알고리즘 : 1Hz로 포인트 클라우드를 매칭하고 정합하여 맵 생성 (low frequency)
두 알고리즘 모두 edge와 planar surface 에 위치한 feature point를 추출하고 각각 edge line segment와 planar surface patch에 매칭한다. odometry 알고리즘에서는 빠른 계산을 보장하기 위해 feature point들의 대응 관계를 찾고, mapping 알고리즘에서는 관련된 고유값과 고유벡터를 통해 로컬 포인트 클러스터의 geometric distribution을 계산해 대응 관계를 결정한다.
SLAM 문제를 odometry와 mapping 문제로 분해하여 더 쉬운 문제인 online motion estimation 을 먼저 풀고, 이후에 높은 정확도의 모션 추정과 맵 생성을 위해 ICP와 유사한 batch optimization을 수행한다. mapping 알고리즘은 lower frequency로 수행되므로 많은 수의 feature point를 포함할 수 있고 수렴을 위해 충분한 반복을 수행할 수 있다.

2. Related Work
motion distortion 무시
라이다의 scan rate가 라이다의 extrinsic motion에 비해 높기 때문에, 스캔 내부의 motion distortion을 무시할 수도 있다. 이 경우 standard ICP mathod 를 사용해 여러 스캔 사이의 laser return 값을 매칭한다.
two-step method
VICP는 two-step method로 distortion을 제거한다. velocity estimation step 후 계산 된 velocity를 이용해 distortion compensation step을 진행한다. Velodyne SLAM에서는 이와 비슷한 방법을 single-axis 3D lidar에 적용해 distortion을 보상한다. 그러나 scanning rotation이 느린 경우 motion distortion이 매우 심해질(severe) 수 있다. 특히 2-axis lidar는 한 축이 다른 축보다 훨씬 느리기 때문에 이런 성향이 강하다.
다른 센서 사용
distortion을 제거할 수 있는 속도 관측값을 얻기 위해 다른 센서를 사용하기도 한다. 예를 들어 IMU를 함께 사용한 visual odometry로부터의 상태 추정을 이용해 라이다 클라우드를 정합할 수 있다. GPS/INS, wheel encoder와 같은 여러 센서의 사용이 가능해지며 EKF나 particle filter를 이용하기도 한다. 이러한 방법은 로봇 네비게이션에서 실시간으로 맵을 생성할 수 있으며 패스 플래닝과 충돌 회피에 사용할 수 있다.
feature matching & linear motion medel
2-axis lidar가 다른 센서 없이 사용된다면 모션 추정과 distortion 보정은 해결해야 할 문제가 된다. Barfoot은 ground vehicle의 모션을 복구하기 위해서 laser intensity return들에서 visual image를 생성해 image 간의 visually distinct feature를 매칭했다. vehicle motion은 등속(constant velocity) 또는 가우시안 프로세스들로 모델링 될 수 있다. LOAM의 odometry 알고리즘은 constant velocity와 비슷하지만 다른 종류의 feature를 사용하는 linear motion model을 사용한다. 등속과 가우시안 프로세스를 사용하는 방법들은 intensity 이미지들로부터의 visual feature를 포함하고 dense point cloud여야 한다. LOAM은 Cartesian space에서 geometric feature들을 추출하고 매칭하며, cloud density가 비교적 낮아도 된다.
본 논문과 비슷한 접근 방식에는 Bosse와 Zlot의 논문이 있다. 이들은 로컬 포인트 클러스터의 geometric structure들을 매칭하여 포인트 클라우드를 정합하기 위해 2-axis lidar를 사용한다. 또한 지하 광산을 매핑하기 위해 multiple 2-axis lidar를 사용한다. IMU를 함께 사용하며, large map을 구성하기 위해 loop closure를 사용한다. 이들의 다른 논문은 batch optimization을 사용해 실시간에 적용하기가 부적절하다.
3. Notations and Description
본 논문은 3D lidar로부터 수신한 포인트 클라우드로 ego-motion 을 추정하고 맵을 구성한다. lidar는 pre-calibrated 되어있다고 가정한다. 또한 라이다의 각속도와 선속도는 갑작스러운 변화 없이 시간에 따라 smooth하고 continuous 하다고 가정한다. 두 번째 가정은 IMU를 사용하면 필요하지 않다.
좌표계 시스템을 표현하기 위해 우측 대문자 윗첨자를 사용한다. 'sweep'을 라이다가 scan coverage를 한 번 완료한 것으로 정의한다. 우측 아랫첨자 $k, k \in Z^{+}$를 사용해 sweep을 나타내고 sweep $k$ 중에 수신한 포인트 클라우드를 $\mathcal{P}_k$라고 한다. 아래와 같이 두 좌표계를 정의한다.
- 라이다 좌표계 $\{L\}$ 은 원점이 라이다의 geometric center인 3D 좌표계이다. x축은 왼쪽, y축은 위, z축은 앞을 가리킨다. 포인트 $i, i \in \mathcal{P}_k$, in $\left\{L_k\right\}$는 ${X}_{(k, i)}^L$로 나타낸다.
- World 좌표계 $\{W\}$는 $\{L\}$과 initial position이 일치하는 3D 좌표계이다. 포인트 $i, i \in \mathcal{P}_k$, in $\left\{W_k\right\}$는 ${X}_{(k, i)}^W$로 나타낸다.
설정한 가정들과 notiation들로 lidar odometry and mapping problem을 정의하면,
Problems : 라이다 클라우드 $\mathcal{P}_k, k \in Z^{+}$의 시퀀스가 주어졌을 때, 각 sweep $k$ 에서의 라이다 ego-motion을 계산하고 $\mathcal{P}_k$로 맵을 구축한다.
4. System Overview
A. LiDAR Hardware
본 연구는 Hokuyo UTM-30LX 레이저 스캐너를 기반으로 하는 커스텀 3D 라이다로 검증하지만, 이에 한정되지는 않는다. 레이저 스캐너는 0.25◦의 해상도와 초당 40 라인의 스캔 속도로 180◦의 FoV를 가진다. 레이저 스캐너에 모터를 연결하고 레이저 스캐너의 수평 방향을 0으로 하여 -90◦ ~ 90◦ 사이에서 초당 180◦의 각속도로 회전한다. 이러한 특정 단위에서, 한 sweep은 -90◦에서 90◦ 로의 회전이나 그 역방향의 회전이다 (1초간 지속). 연속적으로 회전하는 라이다에서 sweep은 단순히 반구형(semi-spherical) 회전이다. 장착된 엔코더는 0.25◦의 해상도로 모터의 회전각을 측정하고 이를 이용해 레이저 포인트들을 라이다 좌표계 $\{L\}$에 투영한다.

B. Software System Overview

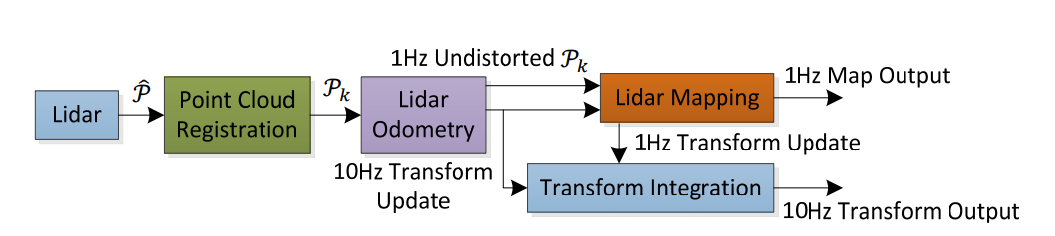
FIg. 3은 소프트웨어 시스템의 다이어그램을 보여준다. 레이저 스캔에서 수신한 포인트들을 $\hat{\mathcal{P}}$라고 하자. 각 sweep에서 $\hat{\mathcal{P}}$은 $\{L\}$에 정합된다. sweep $k$ 중에 누적되는 포인트 클라우드 $k$는 $\mathcal{P}_k$을 구성한다. 그후 $\mathcal{P}_k$은 두 알고리즘에서 처리된다. lidar odometry는 포인트 클라우드를 받아 두 연속적인 sweep 사이의 라이다 모션을 계산한다. 추정된 모션은 $\mathcal{P}_k$ 의 distortion을 보정하는 데 사용한다. 알고리즘은 약 10Hz의 주파수로 수행한다. output은 이후 lidar mapping로 입력되어 1Hz의 주파수로 unidstorted 클라우드를 map에 매칭하고 정합한다. 최종적으로, map에 대한 라이다 포즈를 고려하여 두 알고리즘에서 얻은 pose transform을 통합해 약 10Hz로 transform output을 생성한다.
5. LiDAR Odometry
A. Feature Point Extraction
라이다 클라우드 $\mathcal{P}_k$에서 feature point를 추출한다. Fig. 2의 라이다로 생성한 $\mathcal{P}_k$의 포인트들은 비균일하게 분포되어 있다. 레이저 스캐너는 한 스캔에 0.25◦ 의 해상도를 가진다. 이 포인트들은 스캔 평면에 위치해있다. 그러나 레이저 스캐너가 180◦/s 의 각속도로 회전하며 스캔을 40Hz로 생성하기 때문에 스캔 평면의 수직 방향에서의 해상도는 180◦/40 = 4.5◦ 이다. 이를 고려하여, co-planar geometric 관계를 가진 개별 스캔들의 정보만을 이용해 $\mathcal{P}_k$에서 feature points를 추출한다.
우리는 sharp edges와 planar surface patches에 위치한 feature points를 추출한다. $i$는 $\mathcal{P}_k$ 안의 포인트이고($i \in \mathcal{P}_k$) $\mathcal{S}$는 동일 스캔에서 레이저 스캐너가 반환한 $i$ 주변의 연속적인 포인트 집합이라고 하자. 레이저 스캐너가 CW 또는 CCW 순서로 포인트 반환을 생성하기 때문에, $\mathcal{S}$는 $i$의 양쪽으로 각각 포인트의 절반씩을 포함하며 각 포인트 사이의 간격은 0.25◦이다. 로컬 표면의 smoothness를 평가하는 용어를 $c$로 정의한다.
$$
c=\frac{1}{|\mathcal{S}| \cdot\left\|{X}_{(k, i)}^L\right\|}\left\|\sum_{j \in \mathcal{S}, j \neq i}\left({X}_{(k, i)}^L-{X}_{(k, j)}^L\right)\right\|
$$
스캔에 포함된 포인트들을 $c$ 값을 기반으로 정렬한 후, maximum $c$값을 가진 points는 edge points로, minimum $c$ 값을 가진 points는 planar points로 하여 feature points를 선택한다. 공간 상에서 feature point가 균일하게 분포할 수 있도록 스캔을 네 개의 동일한 subregions으로 나눈다. 각 subregion은 최대 2개의 edge points와 4개의 planar points를 포함할 수 있다. 포인트 $i$는 $c$ 값이 threshold보다 작거나 커야 edge 또는 planar 포인트로 선택될 수 있으며 선택된 포인트들의 숫자는 maximum을 초과할 수 없다.
feature points를 선택함에 있어서, 다음과 같은 포인트들은 피해야 한다.
- 이미 선택된 feature point 주변의 포인트들
- 레이저 빔에 거의 평행한 local planar surfaces 위의 포인트들 (Fig. 4(a)의 point B). 이런 포인트들은 대체로 신뢰성이 떨어진다.
- 가려진(occluded) 영역의 경계에 있는 포인트들. Fig. 4(b)에서 point A 는 연결된 점선 부분의 표면이 다른 객체에 의해 가려져 있기 때문에 edge point로 오판된다. 하지만 라이다가 움직여서 다른 각도로 보면 가려진 구역이 보이게 된다.
위에서 언급한 포인트들을 선택하지 않기 위해, 다시 포인트들의 집합 $\mathcal{S}$를 찾는다. $\mathcal{S}$가 레이저 빔에 평행한 surpace patch를 형성하지 않고, 레이저 빔의 방향으로 $i$와 비연속적인 $\mathcal{S}$ 안의 포인트 중에서 라이다에 $i$보다 더 가까운 포인트가 없을 때(Fig. 4(b)의 point B)만 포인트 $i$를 feature point로 선택할 수 있다.

정리하면, feature point 선택은 edge points는 maximum $c$ 값을 가진 points 부터, planar points는 minimum $c$ 값을 가진 points부터 시작한다. 그리고 포인트가 선택되면,
- 선택된 edge points 또는 planar points는 subregion의 maximum을 초과할 수 없다. 그리고,
- 선택된 포인트 주변에는 이미 선택된 포인트가 없어야 한다. 그리고,
- 선택된 포인트는 레이저 빔에 대략적으로 평행한 surface patch 또는 가려진 부분의 경계 위에 있을 수 없다.
복도 장면에서의 feature points 추출은 Fig. 5.에서 볼 수 있다. edge points와 planar points는 각각 노랑과 빨강으로 표시되어 있다.

B. Finding Feature Point Correspondence
Odometry 알고리즘은 한 sweep 동안의 라이다 모션을 추정한다. 한 sweep $k$의 시작 시간을 $t_k$ 라고 하자. 각 sweep이 끝날 때, sweep 동안의 포인트 클라우드 $\mathcal{P}_k$를 수신하고, Fig. 6에서처럼 time stamp $t_{k+1}$로 재투영한다. 재투영된 포인트 클라우드는 $\overline{\mathcal{P}}_k$로 표기한다. 다음 sweep $k+1$ 동안, $\overline{\mathcal{P}}_k$(초록 선)와 새롭게 수신된 포인트 클라우드 $\mathcal{P}_{k+1}$(주황 선)를 함께 사용해 라이다 모션을 추정한다.

$\overline{\mathcal{P}}_k$와 $\mathcal{P}_{k+1}$을 알고 있다고 가정하고 두 라이다 클라우드 간의 대응관계를 찾자. $\mathcal{P}_{k+1}$에서, 앞서 언급한 방법으로 edge points와 planar points를 추출한다. $\mathcal{E}_{k+1}$와 $\mathcal{H}_{k+1}$는 각각 edge points sets와 planar points sets이다. $\overline{\mathcal{P}}_k$의 edge lines과 $\mathcal{E}_{k+1}$의 points, $\overline{\mathcal{P}}_k$의 planar patches와 $\mathcal{H}_{k+1}$의 points 사이의 대응관계를 찾는다.
sweep $k+1$을 시작할 때 $\mathcal{P}_{k+1}$은 비어 있는 집합이고 sweep이 진행되며 점점 많은 포인트들이 쌓인다. 라이다 odometry는 sweep 중에 6-DoF motion을 반복적으로 추정하고, $\mathcal{P}_{k+1}$이 증가함에 따라 점점 더 많은 포인트들을 포함하게 된다. 각 반복에서 $\mathcal{E}_{k+1}$와 $\mathcal{H}_{k+1}$은 최근에 추정된 transform을 이용해 sweep의 시작 지점으로 재투영된다. 재투영된 point sets는 $\tilde{\mathcal{E}}_{k+1}$와 $\tilde{\mathcal{H}}_{k+1}$ 이다. $\tilde{\mathcal{E}}_{k+1}$와 $\tilde{\mathcal{H}}_{k+1}$의 각 포인트에 대해, $\overline{\mathcal{P}}_k$에서 가장 가까운 이웃 포인트(closest neighbor point)를 찾는다. 이때 $\overline{\mathcal{P}}_k$는 빠른 인덱싱을 위해 3D KD-tree에 저장되어 있다.

Fig. 7(a)는 edge point의 대응인 edge line을 찾는 과정이다. edge feature $i$ 는 $\tilde{\mathcal{E}}_{k+1}, i \in \tilde{\mathcal{E}}_{k+1}$에 대해 대응하는 edge line은 두 개의 포인트로 표현한다. $j$은 $\overline{\mathcal{P}}_k, j \in \overline{\mathcal{P}}_k$에서 $i$의 closest neighbor이다. $l$은 $j$가 있는 스캔의 두 연속적인 스캔에 있는 $i$의 closest neighbor이다. $(i, j)$는 $i$의correspondence 를 구성한다. 그후, $j$와 $l$이 둘 다 edge point인지 검증하기 위해 (1)에 기반하여 local surface의 smoothness를 확인한다.이때, $j$와 $l$이 다른 스캔에서 획득되어야 하는데, 이는 단일 스캔은 동일 edge line에서 하나의 포인트만을 포함할 수 있기 때문이다. 한 가지 예외는 edge line이 scan plane 위에 있을 때인데, 이 경우 edge line은 degenerated 되어 scan plane에서 직선처럼 나타나고 edge line 위의 feature point 들은 처음부터 추출되지 않았을 것이다.
Fig. 7(b)는 planar point의 대응인 planar patch를 찾는 과정이다. planar featrue $i$는 $\tilde{\mathcal{H}}_{k+1}, i \in \tilde{\mathcal{H}}_{k+1}$에 대응하는 planar patch는 세 개의 포인트로 표현한다. edge point와 비슷하게 $\overline{\mathcal{P}}_k$ 안의 $i$의 closest neighbor를 $j$라고 한다. 이제 $i$의 또 다른 closest neighbor 포인트 $l$과 $m$을 찾는다. 하나는 $j$와 같은 스캔, 다른 하나는 $j$의 스캔에 연속적인 두 스캔에서 찾는다. 이는 세 개의 포인트가 non-colinear 하도록 보장한다. $j, l, m$이 모두 planar point 임을 검증하기 위해 (1)에 기반해 local surface의 smoothness를 다시 확인한다.
찾은 feature point 대응관계를 사용해 feature point에서 대응선/면까지의 거리를 계산한다. 다음 section에서는 feature point의 전체적인 거리를 최소화 하여 라이다 모션을 구하게 된다. 먼저 edge point의 거리를 계산한다. 포인트 $i \in \tilde{\mathcal{E}}_{k+1}$에 대해 $(j, l)$이 corresponding edge line 이면 ($ j,l \in \overline{\mathcal{P}}_k$) point-to-line distance는 다음과 같이 계산할 수 있다.
\begin{align}
d_{\mathcal{E}}=\frac{\left|\left(\tilde{{X}}_{(k+1, i)}^L-\overline{{X}}_{(k, j)}^L\right) \times\left(\tilde{{X}}_{(k+1, i)}^L-\overline{{X}}_{(k, l)}^L\right)\right|}{\left|\overline{{X}}_{(k, j)}^L-\overline{{X}}_{(k, l)}^L\right|}
\tag{2} \end{align}
$\tilde{{X}}_{(k+1, i)}^L, \overline{{X}}_{(k, j)}^L$, $\overline{{X}}_{(k, l)}^L$은 $\{L\}$의 포인트 $i, j, l$의 좌표계이다. 그후 포인트 $i \in \tilde{\mathcal{H}}_{k+1}$에 대해 $(i, j, l)$이 corresponding planar patch라면 ($j, l, m \in \overline{\mathcal{P}}_k$) point-to-plane distance는 다음과 같이 계산할 수 있다.
\begin{align}
d_{\mathcal{H}}=\frac{\left|\begin{array}{c}
\left(\tilde{{X}}_{(k+1, i)}^L-\overline{{X}}_{(k, j)}^L\right) \\
\left(\left(\overline{{X}}_{(k, j)}^L-\overline{{X}}_{(k, l)}^L\right) \times\left(\overline{{X}}_{(k, j)}^L-\overline{{X}}_{(k, m)}^L\right)\right)
\end{array}\right|}{\left|\left(\overline{{X}}_{(k, j)}^L-\overline{{X}}_{(k, l)}^L\right) \times\left(\overline{{X}}_{(k, j)}^L-\overline{{X}}_{(k, m)}^L\right)\right|}
\tag{3}\end{align}
$\overline{{X}}_{(k, m)}^L$은 $\{L\}$ 의 포인트 $m$의 좌표이다.
C. Motion Estimation
라이다 모션은 sweep 동안 일정한 각속도와 선속도로 모델링 된다. 이를 통해 다른 시간에 수신된 포인트들에 대해 한 sweep 내에서 pose transform을 선형 보간(linear interpolate) 할 수 있다. current time stamp를 $t$라고 하고, $t_{k+1}$은 sweep $k+1$의 시작 시간이다. ${T}_{k+1}^L$은 $[t_{k+1}, t]$ 사이의 lidar pose transform이다. ${T}_{k+1}^L$은 라이다의 6-DoF constant rigid motion를 포함한다. (${T}_{k+1}^L = \left[t_x, t_y, t_z, \theta_x, \theta_y, \theta_z\right]^T$). $t_x, t_y, t_z$는 각각 $\{L\}$의 $x-, y-, z-$ 축을 따른 translation이고 $\theta_x, \theta_y, \theta_z$는 오른손 법칙을 따른 회전 각도이다. 포인트 $i, i \in \mathcal{P}_{k+1}$가 주어졌을 때, time stamp는 $t_i$이고 ${T}_{(k+1, i)}^L$은 $[t_{k+1}, t_i]$ 사이의 pose transform이다. ${T}_{(k+1, i)}^L$는 ${T}_{k+1}^L$의 선형 보간(linear interpolation)으로 계산할 수 있다.
\begin{align}
{T}_{(k+1, i)}^L=\frac{t_i-t_{k+1}}{t-t_{k+1}} {T}_{k+1}^L
\tag{4}\end{align}
$\mathcal{E}_{k+1}$, $\mathcal{H}_{k+1}$은 $\mathcal{P}_{k+1}$에서 추출한 feature points이고 $\tilde{\mathcal{E}}_{k+1}$, $\tilde{\mathcal{H}}_{k+1}$은 sweep $t_{k+1}$의 시작 지점으로 재투영한 포인트 집합임을 기억하자. 라이다 모션을 풀기 위해, $\mathcal{E}_{k+1}$와 $\tilde{\mathcal{E}}_{k+1}$, $\mathcal{H}_{k+1}$와 $\tilde{\mathcal{H}}_{k+1}$ 사이의 geometric 관계를 설정해야 한다. (4)의 transform을 이용해 (5)를 유도할 수 있다.
\begin{align}
{X}_{(k+1, i)}^L=\mathbf{R} \tilde{{X}}_{(k+1, i)}^L+{T}_{(k+1, i)}^L(1: 3)
\tag{5}\end{align}
- ${X}_{(k+1, i)}^L$ : $\mathcal{E}_{k+1}$ 또는 $\mathcal{H}_{k+1}$에 속한 포인트 $i$의 좌표
- $ \tilde{{X}}_{(k+1, i)}^L$ : $\tilde{\mathcal{E}}_{k+1}$ 또는 $\tilde{\mathcal{H}}_{k+1}$에 속한 corresponding point
- ${T}_{(k+1, i)}^L(a:b)$ : ${T}_{(k+1, i)}^L$의 $a$번째부터 $b$번째까지의 entries
- $\mathbf{R}$ : 로드리게스 공식으로 정의된 회전 행렬로, (6)과 같이 정의된다.
\begin{align}
\mathbf{R}=e^{\hat{\omega} \theta}=\mathbf{I}+\hat{\omega} \sin \theta+\hat{\omega}^2(1-\cos \theta)
\tag{6}\end{align}
(6)에서 $\theta$는 회전의 크기(magnitude)이다.
\begin{align}
\theta=\left\|{T}_{(k+1, i)}^L(4: 6)\right\|
\tag{7}\end{align}
$\omega$는 회전 방향을 표현하는 단위 벡터이고, $\hat{\omega}$는 $\omega$의 skew symmetric matrix 이다.
\begin{align}
\omega={T}_{(k+1, i)}^L(4: 6) /\left\|{T}_{(k+1, i)}^L(4: 6)\right\|
\tag{8}\end{align}
(2)와 (3)은 $\tilde{\mathcal{E}}_{k+1}$, $\tilde{\mathcal{H}}_{k+1}$에 속한 포인트들 사이의 거리를 계산한다. (2)와 (4)-(8)을 합치면 $\mathcal{E}_{k+1}$의 edge point와 corresponding edge line 사이의 geometric 관계를 유도할 수 있다.
\begin{align}
f_{\mathcal{E}}\left({X}_{(k+1, i)}^L, {T}_{k+1}^L\right)=d_{\mathcal{E}}, i \in \mathcal{E}_{k+1}
\tag{9}\end{align}
비슷하게, (3)과 (4)-(8)을 합치면 $\mathcal{H}_{k+1}$의 planar point와 corresponding planar patch 사이의 geometric 관계를 유도할 수 있다.
\begin{align}
f_{\mathcal{H}}\left({X}_{(k+1, i)}^L, {T}_{k+1}^L\right)=d_{\mathcal{H}}, i \in \mathcal{H}_{k+1}
\tag{10}\end{align}
최종적으로, LM(Levenberg-Marquardt) method를 이용해 라이다 모션을 푼다. $\mathcal{E}_{k+1}$와 $\mathcal{H}_{k+1}$안의 각 feature point에 대해 (9)와 (10)을 쌓아서 비선형 함수 (11)을 구한다. ${f}$의 각 행은 하나의 feature point에 해당하고 ${d}$는 해당 거리값을 가진다.
\begin{align}
{f}\left({T}_{k+1}^L\right)={d}
\tag{11}\end{align}
${T}_{k+1}^L$에 대해 ${f}$의 자코비안 행렬 $J$을 계산한다. ($\mathbf{J}=\partial f / \partial {T}_{k+1}^L$) 그후, ${d}$을 0에 가깝게 최소화하는 비선형 iteration을 통해 (11)을 풀 수 있다. $\lambda$는 LM method로 결정한 factor이다.
\begin{align}
{T}_{k+1}^L \leftarrow {T}_{k+1}^L-\left(\mathbf{J}^T \mathbf{J}+\lambda \operatorname{diag}\left(\mathbf{J}^{\mathrm{T}} \mathbf{J}\right)\right)^{-1} \mathbf{J}^{\mathrm{T}} {d}
\tag{12}\end{align}
D. LiDAR Odometry Algorithm
라이다 odometry 알고리즘은 Algorithm 1. 에서 보이는 것과 같다. 마지막 sweep에서의 포인트 클라우드 $\overline{\mathcal{P}}_k$, 현재 sweep의 커지는 포인트 클라우드 $\mathcal{P}_{k+1}$, 마지막 recursion의 pose transform ${T}_{k+1}^L$ 을 input으로 받는다. 새로운 sweep이 시작되면 ${T}_{k+1}^L$는 0으로 설정된다(line 4-6). 그후, 알고리즘은 $\mathcal{P}_{k+1}$에서 feature points를 추출하여 $\mathcal{E}_{k+1}$, $\mathcal{H}_{k+1}$을 구성한다(line 7). 각 feature point에 대해 $\overline{\mathcal{P}}_k$의 대응관계를 찾는다(line 9-19). 모션 추정은 robust fitting에 적용된다. line 15에서, 알고리즘은 각 feature point에 대해 bisquare weight을 적용한다. 대응관계 까지의 거리가 먼 feature points는 적은 가중치를 갖게 되고, 거리가 threshold 보다 큰 feature points는 outlier로 평가되어 가중치가 0이 된다. 그후 line 16에서, 한 iteration 마다 pose transform을 업데이트 한다. 비선형 최적화는 수렴하거나 maximum iteration number만큼 진행됐을 때 종료된다. 알고리즘이 sweep의 끝에 도달하면 sweep 동안에 추정한 모션을 이용해 $\mathcal{P}_{k+1}$을 time stamp $t_{k+2}$로 재투영한다. 그렇지 않으면 recursion의 다음 round를 위해 transform ${T}_{k+1}^L$만을 반환한다.

6. LiDAR Mapping

mapping 알고리즘은 odometry 알고리즘보다 lower frequency로 실행되고 한 sweep 당 한 번 호출된다. sweep $k+1$이 끝날 때, lidar odometry는 undistorted point cloud $\overline{\mathcal{P}}_{k+1}$와 $[t_{k+1}, t_{k+2}]$ 사이의 sweep 중의 라이다 모션을담고 있는 pose transform ${T}_{k+1}^L$을 동시에 생성한다. mapping 알고리즘은 Fig. 8과 같이 world 좌표계 $\{W\}$에서 $\overline{\mathcal{P}}_{k+1}$을 매칭하고 정합한다.
- $\mathcal{Q}_k$ : $k$ sweep까지 누적된 map 위의 포인트 클라우드
- ${T}_{k}^W$ : sweep $k$가 끝날 때인 $t_{k+1}$에서 map 위에서의 라이다 포즈
lidar odometry의 출력을 이용해 mapping 알고리즘은 ${T}_{k}^W$을 $t_{k+1}$에서 $t_{k+2}$로 한 sweep 확장해 ${T}_{k+1}^W$을 얻을 수 있고 $\overline{\mathcal{P}}_{k+1}$을 world 좌표계 $\{W\}$로 투영해 $\overline{\mathcal{Q}}_{k+1}$라고 표기한다. 그 다음, 알고리즘은 라이다 포즈 $T_{k+1}^W$를 최적화 하여 $\overline{\mathcal{Q}}_{k+1}$을 $\mathcal{Q}_k$와 매칭한다.
feature point는 Section odometry 알고리즘의 5-A와 같은 방식으로 추출하되, 10배 더 많은 feature points를 사용한다. feature points의 대응관계를 찾기 위해 맵의 포인트 클라우드 $\mathcal{Q}_k$를 10m cubic areas로 저장한다. $\overline{\mathcal{Q}}_{k+1}$와 교차하는 cubes 안의 포인트들을 추출해 3D KD-tree에 저장한다. featrue points 주변의 특정 지역에 있는 $\mathcal{Q}_k$에 속한 포인트를 찾는다. $\mathcal{S}'$를 주변 포인트들의 집합이라고 하자. edge point의 경우 $\mathcal{S}'$에 edge lines 위의 포인트만 유지하고 planar point의 경우 planar pathces 위의 포인트만 유지한다. 그후 $\mathcal{S}'$의 공분산 행렬을 계산해 $\mathbf{M}$이라고 한다. $\mathbf{M}$의 고유값과 고유벡터는 각각 $\mathbf{V}$와 $\mathbf{E}$라고 한다. $\mathcal{S}'$이 edge line 위에 분포되어 있다면 $\mathbf{V}$는 다른 두 개보다 현저히 큰 고유값을 가질 것이고 가장 큰 고유값과 연관된 $\mathbf{E}$의 고유벡터는 edge line의 방향을 나타낼 것이다. 한편, $\mathcal{S}'$이 planar patch에 분포되어 있다면, $\mathbf{V}$는 두 개의 큰 고유값보다 현저히 작은 고유값을 가질 것이고, 가장 작은 고유값과 연관된 $\mathbf{E}$의 고유벡터는 planar patch의 방향을 나타낼 것이다. edge line 또는 planar patch의 위치는 $\mathcal{S}'$의 geotetric center를 통과하여 구한다.
feature point에서 그 대응관계 까지의 거리를 계산하기 위해 한 edge line 위의 두 포인트, planar patch위의 세 포인트를 선택한다. 이렇게 하면 (2)와 (3)의 공식을 이용해 거리를 계산할 수 있다. 그후 각 feature point에 대해 (9) 또는 (10)으로 식을 유도할 수 있다. odometry 알고리즘과 다른 점은 $\overline{\mathcal{Q}}_{k+1}$의 모든 포인트가 동일한 time stamp $t_{k+2}$을 공유한다는 것이다. LM method를 통해 robust fitting으로 비선형 최적화를 다시 풀고 $\overline{\mathcal{Q}}_{k+1}$를 map에 정합한다. 포인트들을 균일하게 분포하게 하기 위해, voxel size가 5cm cubes인 voxel grid filter로 map cloud를 downsize 한다.
pose transform의 통합은 Fig. 9에서 묘사한다. 파란 부분은 라이다 매핑에서의 pose output $T_{k}^W$이고 한 sweep 당 한 번 생성된다. 주황색 부분은 라이다 odometry 에서의 transform output ${T}_{k+1}^L$이고 약 10Hz의 frequency이다. map에 대한 라이다 포즈는 라이다 odometry와 동일한 frequency(10Hz)에서 두 transform의 결합이다.

7. Experiments
odometry 와 mapping 프로그램은 개별 코어에서 실행된다.
A. Indoor & Outdoor Tests

맵의 local 정확도를 평가하기 위해, 데이터 선택 중에 몇몇 위치에서 가만히 있는 포인트 클라우드를 획득했다. 두 포인트 클라우드는 ICP method를 이용해 매칭하고 비교했다. 매칭이 끝나면 한 포인트 클라우드와 두번째 포인트 클라우드의 corresponding planar patches 사이의 거리를 매칭 에러로 사용한다. FIg. 11은 에러 분포의 밀도를 보여준다. 실내 환경이 실외보다 적은 매칭 에러를 보인다. 자연 환경에서의 feature matching이 manufactured 환경에서보다 덜 정확하므로 합리적인 결과이다.

추가적으로 모션 추정의 누적 드리프트를 측정하는 테스트를 진행했다. 실내 환경은 closed loop를 포함한 corridor를 선택하여 시작 지점과 끝 지점이 같도록 한다. 모션 추정은 시작과 끝 위치 사이에 차이가 존재하도록 하게 하므로 드리프트의 양을 알 수 있다. 실외 환경에서는 orchard 환경을 선택했다. ground vehicle은 높은 정확도의 GPS/INS를 ground truth 획득에 사용할 수 있다. 측정된 드리프트는 이동 거리에 따라 relative accuracy로 Table 1에 나열되어 있다. 특히 Test 1은 Fig. 10(a), Fig. 10(g)와 같은 데이터셋을 사용한다. 일반적으로 실내 테스트의 relative accuracy는 약 1%이고 실외 테스트는 약 2.5% 이다.

B. Assistance from an IMU
빠른 속도 변화를 다루기 위해 라이다에 Xsens MTi-10 IMU를 붙였다. LOAM에 보내기 전에 포인트 클라우드를 두 가지 방법으로 전처리 한다. 1) IMU로 얻은 orientation을 이용해, 한 sweep에서 수신된 포인트 클라우드를 해당 sweep의 라이다 initial orientation해 알맞게 회전한다. 2) 가속도 측정값을 이용해, 마치 sweep 중에 라이다가 등속으로 이동하는 것처럼 motion distortion을 부분적으로 제거한다. 이후 포인트 클라우드는 lidar odometry와 mapping 프로그램에 의해 처리된다. IMU orientation은 gyro로부터 얻은 angular rates와 accelerometer를 칼만 필터로 통합해 얻는다. Fig. 12(a)는 샘플 결과를 보여준다. 한 사람이 라이다를 들고 계단을 걷는다. 빨간선을 계산할 때 IMU로 orientation을 얻고 LOAM으로 translation 만을 추정한다. orientation은 데이터 수집을 하는 5분 동안 25◦ 이상의 drift가 발생했다. 초록선은 LOAM의 최적화만을 이용했고 IMU는 사용하지 않았다. 파란선은 전처리에 IMU 데이터를 사용하고 이후 LOAM을 적용했다. 파란선과 초록선 사이에서 작은 차이를 볼 수 있다. Fig. 12(b)는 파란선에 해당하는 맵이다. Fig. 12(c)에서는 Fig. 12(b)에서 노란 네모로 표시한 구역의 확대를 비교한다. 상단의 그림은 파란선에 해당하고 하단의 그림은 초록선에 해당한다. 상단의 그림에서 edge가 더 날카롭다.

Table 2는 IMU 사용 여부에 따른 모션 추정의 relative error를 비교한다.사람이 라이다를 들고 0.5m/s의 속도로 걷고 라이다는 위아래로 약 0.5m의 크기만큼 움직인다. ground truth는 줄자로 직접 측정했다. 네 개의 테스트에서 IMU의 도움을 받은 LOAM이 가장 높은 정확도를 달성했고 IMU만으로 orientation을 추정한 것이 가장 낮은 정확도를 보였다. 선형 모션을 다루는 LOAM과 함께, IMU는 비선형 모션을 상쇄하는 데 효과적이다.

C. Tests with KITTI Datasets
자동차에는 360◦ Velodyne lidar, 컬러/흑백 스테레오 카메라, ground truth를 위한 높은 정확도의 GPS/INS가 달려 있다. 라이다 데이터는 10Hz로 로깅되며 odometry 추정에 사용된다. 공간 문제로 결과는 포함하지 않지만 벤치마크 웹사이트에서 확인 가능하다. 평균 postion 에러는 이동 거리에 대해 0.88%이다.
